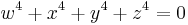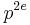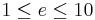Supersingular K3 surface

In algebraic geometry, a supersingular K3 surface is a K3 surface whose l-adic cohomology is generated by algebraic cycles; in other words, since the second Betti number of a K3 surface is always 22, such a surface must possess 22 independent elements in its Picard group (ρ = 22).

Such surfaces can exist only in positive characteristic, since in characteristic zero Hodge theory gives an upper bound of 20 independent elements in the Picard group. In fact the Hodge diamond for any complex K3 surface is the same (see classification) and the middle row reads 1, 20, 1. In other words h2,0 and h0,2 both take the value 1, with h1,1 = 20. Therefore the dimension of the space spanned by the algebraic cycles is at most 20 in characteristic zero; surfaces with this maximum value are called singular K3 surfaces.

Contents

History

The first example was given by Tate (1965), who observed that the Fermat quartic

w^4%2Bx^4%2By^4%2Bz^4=0\

is a supersingular K3 surface over fields of characteristic 3 mod 4. Their theory was developed by Michael Artin (1974) and Tetsuji Shioda. Artin conjectured that every supersingular K3 surface is unirational; this conjecture remains open as of 2007. Shimada (2004, 2004b) has shown that supersingular K3 surfaces are double covers of the projective plane. In the case of characteristic 2 the double cover may need to be an inseparable covering.

Artin's conjecture has been shown to be true in characteristic two by Rudakov & Shafarevich (1978) and more recently by Shimada. The conjecture remains open in characteristic three; several families of examples have been constructed, showing that it is at least plausible.

The discriminant of the intersection form on the Picard group of a supersingular K3 surface is an even power

p^{2e}

of the characteristic p, as was shown by Michael Artin and James S. Milne. Here e is defined to be the Artin invariant. We have

1 \le e \le 10\

as was also shown by Michael Artin. There is a corresponding Artin stratification.

Examples

The elliptic modular surface of level 4 for characteristic 3 mod 4 is supersingular, as is the Kummer surface of a product of 2 supersingular elliptic curves in odd characteristic.

In characteristic two,

z2 = f(x, y) ,

for a sufficiently general polynomial f(x, y) of degree six, defines a surface with twenty-one isolated singularities. It can be shown that the smooth projective minimal model of the function field of such a surface is a supersingular K3 surface. The largest Artin invariant here is ten.

Similarly, in characteristic three,

z3 = g(x, y) ,

for a sufficiently general polynomial g(x, y) of degree four, defines a surface with nine isolated singularities. It can be shown that the smooth projective minimal model of the function field of such a surface is again a supersingular K3 surface. The highest Artin invariant in this family is six.

In characteristic five,Pho & Shimada (2006) demonstrated that every supersingular K3 surface with Artin invariant less than four is birationally equivalent to a surface with equation

z5 = h(x, y) ,

and thus every such surface is unirational.

Kummer surfaces

If the characteristic p is greater than 2, all supersingular K3 surfaces S with Artin invariant 0, 1 and 2 are birationally Kummer surfaces, in other words quotients of an abelian surface A by the mapping x → − x. More precisely, A should be a supersingular abelian surface, isogenous to a product of two supersingular elliptic curves. Ogus (1979) showed that the Kummer surface is singular; the construction of S is as a minimal resolution. Shimada & Zhang (2007) made an extension to p = 2 with a group scheme quotient.

References